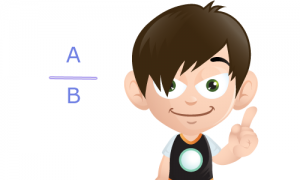Ce cours sur les fractions ressemble beaucoup aux divisions. Croyez-moi, les divisions c’est utile et surtout très facile à utiliser !
Une fraction est tout simplement un nombre qui s’écrit de la manière suivante :
Totomaths.fr
A et B étant deux nombres entiers avec B différent de zéro.
On dit aussi que A est le numérateur et que B est le dénominateur.
Remarque : On ne change pas la valeur d’une fraction si on divise ou si on multiplie le numérateur et le dénominateur par un même nombre non nul.
Quoi encore Toto ? Tu n’as pas compris ce que je viens de dire ? C’est pourtant simple 
Par exemple, si j’ai la fraction suivante : 2/3
Je sais que 2/3 = (2*5)/(3*5) = (2*9)/(3*9)
Ne me dite pas c’est bizarre ou c’est magique… C’est logique !
Reprenons l’exemple ci-dessus : 2/3 = (2*5)/(3*5)
Je sais que 2*5 = 10
Je sais aussi que 3*5 = 15
Alors 2/3 = 10/15 !
Totomaths.fr
Simplification des fractions. :
Imaginons que l’on me demande de simplifier la fraction suivante : 10/15
Comment vais-je faire ?
L’idée est de « trouver » un même nombre dont le numérateur et le dénominateur sont multiple.
Je m’explique : 10 = 5*2 et 15 = 5*3. J’ai donc trouver ce même nombre : 5.
Passons maintenant à un exemple de calcul. Par exemple, je souhaite calculer (2/3) * 6.
En fait pour réaliser ce calcul, j’ai besoin d’avoir à chaque fois un numérateur et un dénominateur. Le problème c’est que 6 n’a pas de dénominateur. Dans ces cas là, je dirais toujours que 6=6/1. Génial ! Je peux donc faire mon calcul :
J’obtiens donc l’opération suivante :
(2/3) * (6/1) = (2*6) / (3*1) = 12/3
Dans un multiplication, je multiplie les numérateurs entre eux et les dénominateurs entre eux.
Totomaths.fr
Par contre dans le cas d’une addition c’est différent, je dois avoir systématiquement le même dénominateur pour pouvoir les additionner. Par exemple (2/3) + 6.
Je sais que 6 = 6/1 = (6*3)/(1*3) = 18/3.
Génial ! J’ai le même dénominateur.
J’obtiens l’opération suivante :
(2/3) + (18/3) = (2+18) / 3 = 20/3
Avec les additions j’additionne uniquement les numérateurs, je ne touche pas au dénominateur !
Bon courage !